Programowanie

Algorytm - jednoznaczny przepis obliczenia w skończonym czasie pewnych danych wejściowych do pewnych danych wynikowych.

Przykład

Znalezienie największej wśród niepustej, nieposortowanej listy przypadkowych liczb można przeprowadzić na wiele sposobów, jednym z najszybszych jest przedstawiony niżej. Niech  oznacza wskazuje aktualnie badany element listy (jeśli jest ona numerowana, może on oznaczać np. jej numer), a  oznacza największą dotychczas znalezioną wartość.

1. Niech  wskazuje na pierwszy element (początek) listy.
2. Niech  zawiera wartość elementu listy wskazywanego przez  (tzn. pierwszego).
3. Jeżeli zawartość elementu listy wskazywanego przez  jest większa od zawartości 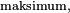 to przypisz  wartość elementu wskazywanego przez 
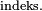
4. Niech  wskazuje kolejny element listy; jeśli to niemożliwe (tzn.  wskazuje ostatni element listy, czyli jej koniec), przejdź do punktu 6.
5. Wróć do punktu 3.
6. Koniec.

Wykonanie tego algorytmu spowoduje, że największa liczba na wspomnianej liście będzie wartością 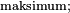 ciekawostką jest fakt, iż algorytm ten działa dla list dowolnej długości (nie wykorzystuje on liczby elementów listy, lecz tylko tzw. operację następnikadanej listy, tzn. przejścia do następnego jej elementu; niemożność wskazania kolejnego elementu jest wtedy równoważna temu, iż dany element jest ostatni na liście).

Klasyfikacja

Istnieje wiele różnych sposobów podziału algorytmów na grupy. Problem ten wzbudza kontrowersje.

Podstawowe paradygmaty tworzenia algorytmów komputerowych:

Istnieje wiele różnych sposobów podziału algorytmów na grupy. Problem ten wzbudza kontrowersje.

Podstawowe paradygmaty tworzenia algorytmów komputerowych:

- dziel i zwyciężaj – dzielimy problem na kilka mniejszych, a te znowu dzielimy, aż ich rozwiązania staną się oczywiste,

- programowanie dynamiczne – problem dzielony jest na kilka, ważność każdego z nich jest oceniana i po pewnym wnioskowaniu wyniki analizy niektórych prostszych zagadnień wykorzystuje się do rozwiązania głównego problemu,

- metoda zachłanna – nie analizujemy podproblemów dokładnie, tylko wybieramy najbardziej obiecującą w tym momencie drogę rozwiązania,

- programowanie liniowe – oceniamy rozwiązanie problemu przez pewną funkcję jakości i szukamy jej minimum,

- poszukiwanie i wyliczanie – kiedy przeszukujemy zbiór danych aż do odnalezienia rozwiązania,

- heurystyka – człowiek na podstawie swojego doświadczenia tworzy algorytm, który działa w najbardziej prawdopodobnych warunkach, rozwiązanie zawsze jest przybliżone.

Najważniejsze techniki implementacji algorytmów komputerowych:

- proceduralność – algorytm dzielimy na szereg podstawowych procedur, wiele algorytmów współdzieli wspólne biblioteki standardowych procedur, z których są one wywoływane w razie potrzeby,

- praca sekwencyjna – wykonywanie kolejnych procedur algorytmu, według kolejności ich wywołań, na raz pracuje tylko jedna procedura,

- praca wielowątkowa – procedury wykonywane są sekwencyjnie, lecz kolejność ich wykonania jest trudna do przewidzenia dla programisty

- praca równoległa – wiele procedur wykonywanych jest w tym samym czasie, wymieniają się one danymi,

- rekurencja – procedura lub funkcja wywołuje sama siebie, aż do uzyskania wyniku lub błędu,

- obiektowość – procedury i dane łączymy w pewne klasy reprezentujące najważniejsze elementy algorytmu oraz stan wewnętrzny wykonującego je urządzenia,

- algorytm probabilistyczny – algorytm działa poprawnie z bardzo wysokim prawdopodobieństwem, ale wynik nie jest pewny,